Veamos cómo ubicar fracciones en la recta numérica.

 Verás que es muy fácil. 

Primero
recordemos los términos de una fracción: 

Numerador y denominador

Por ejemplo, una fracción: 

$\frac{3}{4}$ Entendida así:  $\frac{3}{4}$

Gráficamente: 

Segundo
¿Cómo ubicar fracciones en la recta numérica?

Por ejemplo, para representar la fracción $\frac{3}{4}$ (un tercio), el segmento entre 0 y 1 se divide en 3 partes iguales (como indica el denominador) y se considera 1 de ellas (como indica el numerador), pero siempre partiendo desde el 0.

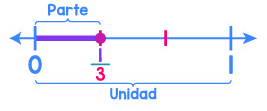
Para representar la fracción $\frac{3}{4}$ (dos tercios), el segmento entre 0 y 1 se divide en 3 partes iguales y se consideran 2 de ellas, partiendo desde el 0 y avanzando a la derecha.

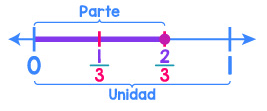
Cuando el numerador y el denominador son iguales, entonces la fracción es igual a la unidad o 1.

Por eso, la fracción $\frac{3}{4}$ (tres tercios) cae sobre el 1. También, puedes partir el segmento entre 0 y 1 en 3 partes iguales y considerar 3 de ellos.

 

Si queremos ubicar la fracción $\frac{3}{4}$ (cuatro tercios) en la recta numérica, tomamos el segmento entre 0 y 1 y lo dividimos en 3 partes iguales.

Sin embargo, debemos tomar 4 partes, como no tenemos suficientes partes, avanzamos al segmento entre 1 y 2 y lo dividimos también en 3 partes iguales.

Luego tomamos 4 partes partiendo desde el 0 a la derecha.

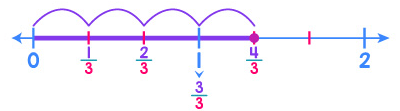
Siguiendo los mismos pasos, podemos ubicar la fracción $\frac{3}{4}$.