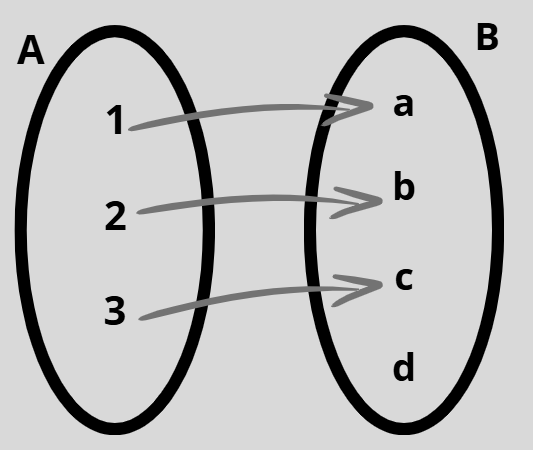
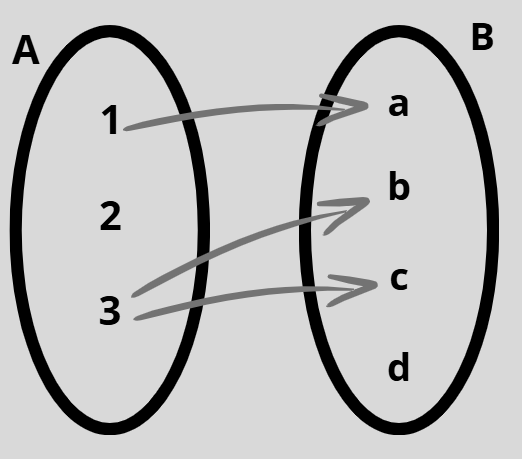
¿Qué son las funciones?
Definición
Sean A y B dos conjuntos.
Una función ƒ de A en B es una relación que asigna a cada elemento x de un conjunto A un único elemento del conjunto B.
ƒ(α) = b si b es el único elemento de B asignado por la ƒ al elemento α de A.
Si ƒ es una función de A en B se escribe ƒ:A → B