Área y volumen de una esfera
Para calcular la superficie de los poliedros y de algunos cuerpos de revolución, hay que hacer su desarrollo plano y a partir de él, se obtiene la superficie; pero con la esfera hay un problema... ¡no se puede desarrollarla sobre el plano más que por una aproximación!
Entonces, ¿cómo se puede calcular su superficie? ¿Y su volumen?
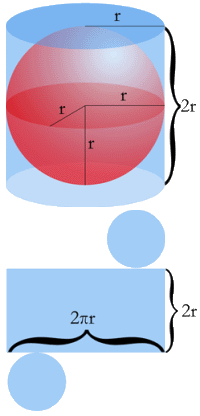
Arquímedes demostró que el área de una esfera es igual al área lateral de un cilindro que tenga el mismo radio y cuya altura sea el diámetro de la esfera.
La imagen muestra una esfera envuelta por un cilindro que se ajusta por completo a ella, un cilindro de radio R y altura 2R.
Tenemos entonces que el área de la esfera es igual al área lateral de ese cilindro:
A Esfera = A Lateral del cilindro = 2
R x 2R = 4R2
Ahora vamos a imaginarnos que llenamos el espacio que no está ocupado en el cilindro con agua.
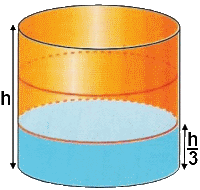Si sacamos la esfera y nos fijamos en la cantidad de agua que hay, veremos que solo ocupa la tercera parte del cilindro.
Tenemos entonces que la esfera solo ocupa las dos terceras partes del volumen del cilindro que la contiene:
V Esfera = 2/3 V Cilindro = 2/3 x R2 x 2R = 4/3 R3
Esta fórmula fue descubierta por Arquímedes, quien demostró que el volumen de la esfera es igual a dos tercios del volumen del cilindro circular circunscrito a ella.
Tanto lo impresionó esto que mandó grabar en su tumba esta figura en recuerdo de la mejor de sus ideas: 
Obra publicada con Licencia Creative Commons Reconocimiento No comercial Compartir igual 4.0