Como vimos el,
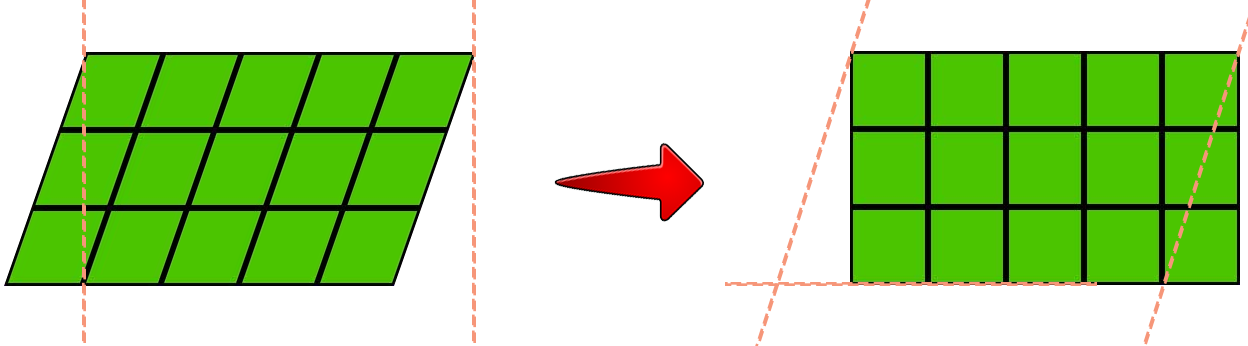
área del rectángulo
Tras contar las unidades de 1 cm2 que lo integran, es de 15 cm2... Pero también podemos ver que ese es el resultado del producto de la medida de su base por su altura.
Es decir, en el eje horizontal hay 5 unidades de 1 cm2 y en el vertical 3... 3 x 5 = 15.
Entonces, podemos afirmar que:
Área rectángulo = base (b) x altura (h)
Podemos hacer el mismo razonamiento con el
área del cuadrado
En el cuadrado, al ser iguales la base y la altura, tiene por área su lado al cuadrado (lado por lado).
En el caso que vemos, sería: 3 x 3 = 9... El área del cuadrado es de 9 cm2
Entonces, podemos afirmar que:
Área cuadrado = lado (l) x lado (l)
(o, de otra forma = lado2)
El caso del
área del romboide
El romboide se puede transformar en un rectángulo...
Por lo cual su área también es el producto de su base por su altura.
Entonces, podemos afirmar que:
Área romboide = base (b) x altura (h)
El caso del
área del rombo
Si insertamos el rombo en un rectángulo
Veremos que su base es igual a la diagonal mayor del rombo (D) y su altura es igual a la diagonal menor (d). Observaremos así que el área del rombo es la mitad del área de ese rectángulo (el rectángulo amarillo cuadriculado de 5 x 3, en este caso).
Entonces, si vimos que el área del rectángulo es base (b) por altura (h); entonces, el área del rombo será la mitad de esa ecuación.
Es decir, en este caso:
Entonces, podemos afirmar que:
Área rombo = base (b) x altura (h)
2
(base (b) x altura (h) / 2)
El caso del
área del triángulo
Si trazamos paralelas a los lados opuestos a la base del triángulo obtenemos un romboide:
El triángulo es la mitad de un romboide.
Si el área del romboide es base (b) por altura (h), entonces el área del triángulo, que es la mitad, también será la mitad.
Es decir, en este caso es:
Entonces, podemos afirmar que:
Área triángulo = base (b) x altura (h)
2
(base (b) x altura (h) / 2)
El caso de los
polígonos regulares
Cualquier polígono regular se puede descomponer en tantos triángulos iguales como número de lados tiene. Tan solo tenemos que unir sus vértices con el centro.
El área de un polígono regular será entonces igual a la suma del área de todos los triángulos que se forman.
Si movemos los triángulos y los acomodamos formaremos un romboide:
Entonces, podemos encontrar el área del polígono como si calculásemos el de un romboide o calculando el de cada triángulo y multiplicarlo por 6.
Obra publicada con Licencia Creative Commons Reconocimiento No comercial Compartir igual 4.0