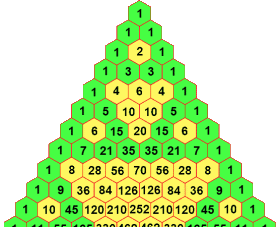
Si coloreamos de distinto color los números pares e impares del Triángulo de Pascal, veremos que sigue una distribución semejante a la del Triángulo de Sierpinski, si imaginamos el Triángulo de Pascal infinitamente grande.
Los números pares serían los triángulos que vamos eliminando en el triángulo en cada iteración.
¡Una curiosa relación!
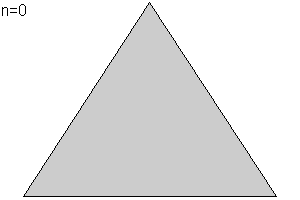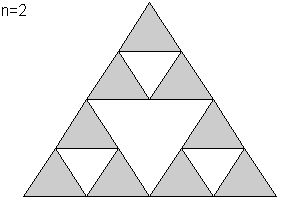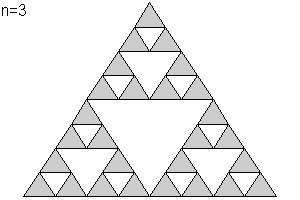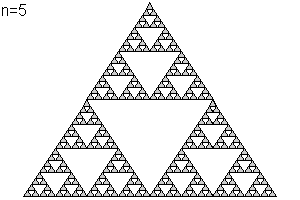
¿Cómo se construye el Triángulo de Sierpinski?
Se parte de un triángulo equilátero, se marcan los puntos medios de cada lado y se construye a partir de ellos un triángulo equilátero invertido. Se repite el proceso con cada uno de los tres triángulos que quedan, ¡y así infinitamente!