Para todo triángulo rectángulo

El resultado anterior lo podemos generalizar para todo triángulo rectángulo.

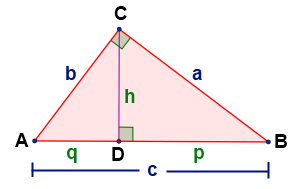Observa el dibujo

Si trazamos la altura h sobre la hipotenusa c de un triángulo rectángulo y consideramos los segmentos p y q que la altura determina sobre la hipotenusa, correspondientes a las proyecciones de los catetos a y b respectivamente, obtenemos:

Δ ABC ~ Δ CBD, porque
ACB = CDB = 90º y     
CBA = DBC, entonces por el criterio AA, los triángulos son semejantes.

Δ ABC ~ Δ ACD, porque
ACB = ADC = 90º y
CAB = DAC, entonces por el criterio AA, los triángulos son semejantes.

Por lo tanto, los tres triángulos son semejantes.
Entonces,
Δ ABC ~ Δ CBD ⇒ 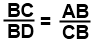⇒ ⇒ a² = p · c
Δ ABC ~ Δ ACD ⇒ ⇒ ⇒ b² = q · c
Δ CBD ~ Δ ACD ⇒ 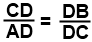⇒ ⇒ h² = p · q

Obtuvimos tres relaciones importantes sobre los triángulos rectángulos.
Estas relaciones son conocidas como el teorema de Euclides.