Este proceso puede realizarse de manera general; corresponde a la generalización del Teorema de Pitágoras y es conocido como Teorema del Coseno.
Observa:
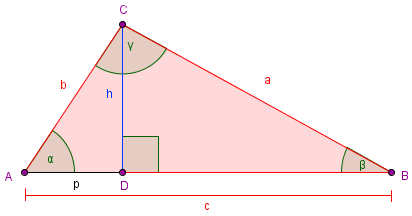
En el triángulo de la figura, trazamos la altura h sobre el lado c. Si llamamos p a la proyección del lado b sobre la hipotenusa, del mismo modo que en el problema anterior, tendremos que:
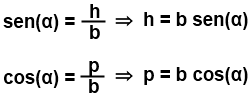
Luego, por el Teorema de Pitágoras, también tenemos que a2 = h2 + (c - p)2, donde podemos remplazar los valores encontrados para h y p.
Observa:
a2 = h2 + (c - p)2
= (b sen(α))2 + (c - b cos(α))2
= b2 sen2(α) + c2 - 2bc cos(α) + b2 cos2(α)
↓
Remplazamos recordando la identidad: cos2(α) + sen2(α) = 1
Luego,
a2 = b2 + c2 - 2bc cos(α)
Este resultado se conoce como Teorema del Coseno.