¿Por qué únicamente 5?

Como has visto, un poliedro es regular si:

• Sus caras son polígonos regulares iguales.
• En cada vértice concurre el mismo número de polígonos.

Para que se forme un poliedro en cada vértice deben concurrir 3 o más caras y la suma de los ángulos que concurren en cada vértice ha de ser menor de 360°.

Si la suma es 360° se forma un mosaico que recubre el plano.

Analiza la siguiente tabla:

Polígono regular	N° polígonos por vértice	Vértice del poliedro	Poliedro regular
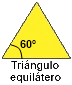
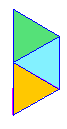
	3 x 60° = 180° < 360°
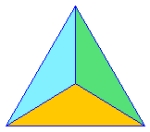
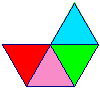
	4 x 60° = 240°< 360°
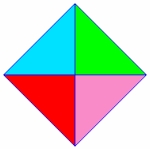
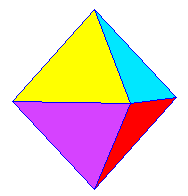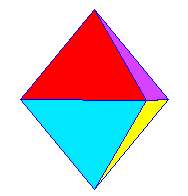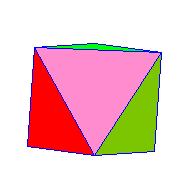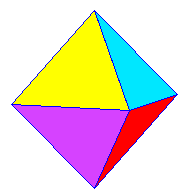
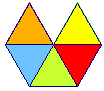
	5 x 60° = 300°< 360°
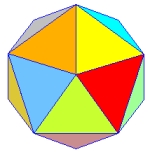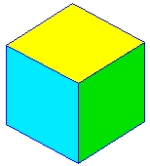
	3 x 90° = 270°< 360°
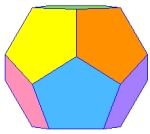
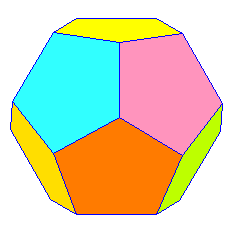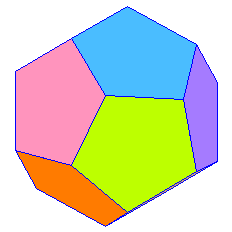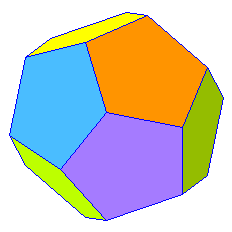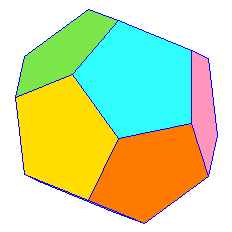
	3 x 108° = 324° < 360°

Si utilizáramos 6 triángulos equiláteros la suma de los ángulos que concurren en cada vértice es igual a 360°. Lo mismo ocurre con 4 cuadrados y en estos casos no se puede formar un poliedro, se forman mosaicos que cubren el plano:

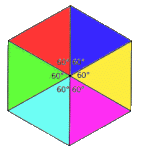
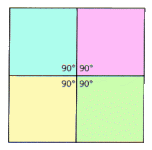
Con polígonos de mayor número de lados tampoco es posible formar poliedros. Con 3 hexágonos regulares se forma también un mosaico:

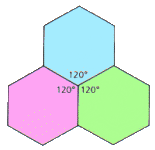
Por lo tanto, concluimos que únicamente se pueden formar 5 poliedros regulares: tetraedro, octaedro, icosaedro, hexaedro y dodecaedro.