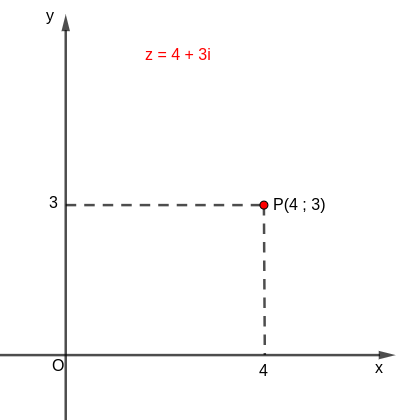
Un número complejo está determinado cuando se conoce su parte real y su parte imaginaria; es decir el complejo está definido cuando se identifican sus dos componentes que son además números reales.

Así, al complejo  le podemos asociar la pareja de números reales  que lo determinan.

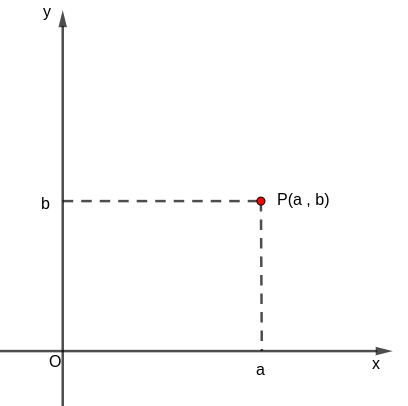
A este par ordenado  lo podemos representar en un sistema de ejes coordenados cartesianos, en donde en el eje de abscisas indicamos la componente real , y en el eje de ordenadas, la componente imaginaria  del complejo.

De esta forma, a cada número complejo  le asignamos un único punto del plano de coordenadas , y recíprocamente a cada punto del plano de coordenadas  le corresponde un único complejo. Se establece así una función biyectiva entre los números complejos y los puntos del plano.

Nombramos:  es el eje real  y   es el eje imaginario

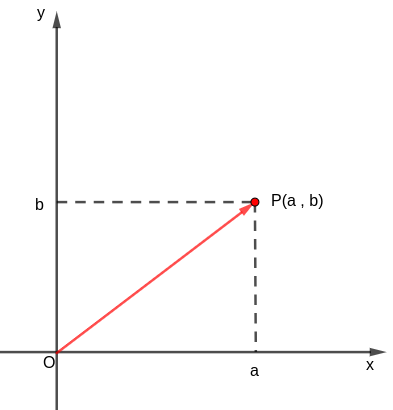
 es el afijo del complejo  y , es el vector asociado a  

Ejemplo: