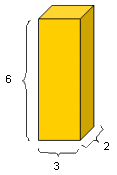
El volumen del paralelepípedo recto se calcula multiplicando las longitudes de las tres aristas convergentes a un vértice. Por ejemplo, si las aristas de un paralelepípedo recto son 2, 3 y 6 cm, entonces el volumen de este se obtiene multiplicando 2 x 3 x 6:
V = 2cm x 3cm x 6cm = 36cm³
Por lo tanto, si las tres aristas concurrentes a un vértice miden a, b y c, entonces su volumen se calcula a través de la fórmula:
V = a.b.c
El volumen de un paralelepípedo se puede también definir como el producto del área de la base por la altura, es decir:
En el ejemplo: V = (3cm x 2 cm) x 6 cm = 6cm² x 6cm = 36cm³
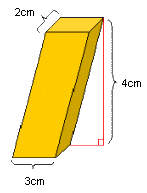Si el prisma no es recto, su volumen, según el principio de Cavalieri, será el mismo que el del prisma recto con igual sección y altura. La única diferencia es que, en este caso, la altura no coincide con la arista lateral.
Por ejemplo, si las aristas de la base de un paralelepípedo oblicuo miden 3 cm y 2 cm, y su altura mide 4 cm, entonces su volumen se calcula a través de la fórmula del paralelepípedo recto:
V = (3cm x 2cm) x 4cm = 6cm² x 4cm = 24cm³