Para demostrar que ![]() era un número irracional, los griegos razonaron dando una demostración por reducción al absurdo.
era un número irracional, los griegos razonaron dando una demostración por reducción al absurdo.
Observa:
Si existiera un racional igual a ![]() , se escribiría como una fracción x/y , con x e y números enteros positivos.
, se escribiría como una fracción x/y , con x e y números enteros positivos.
Supongamos que simplificamos todos los factores comunes entre x e y, de modo que obtenemos la fracción a/b, que es irreducible.
Pero de ![]() = a/b se obtiene
= a/b se obtiene ![]() . b = a, de donde se deduce, elevando al cuadrado, que 2b2 = a2. Entonces, 2 divide el número entero a2 y como 2 es número primo, 2 divide a a, por lo que a2 es múltiplo de 4, es decir, a2 = 4k, con k algún número entero.
. b = a, de donde se deduce, elevando al cuadrado, que 2b2 = a2. Entonces, 2 divide el número entero a2 y como 2 es número primo, 2 divide a a, por lo que a2 es múltiplo de 4, es decir, a2 = 4k, con k algún número entero.
Luego, para b se cumple 2b2 = 4k, de donde b2 = 2k, o sea, b2 es múltiplo de 2, el que es primo, por lo que 2 divide a b, pero entonces 2 divide a a y a b, aun si no tenían factores comunes, lo cual es una contradicción. Entonces, la suposición de que ![]() es un número racional es incorrecta.
es un número racional es incorrecta.
- Por lo tanto,
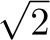 es un número irracional.
es un número irracional.