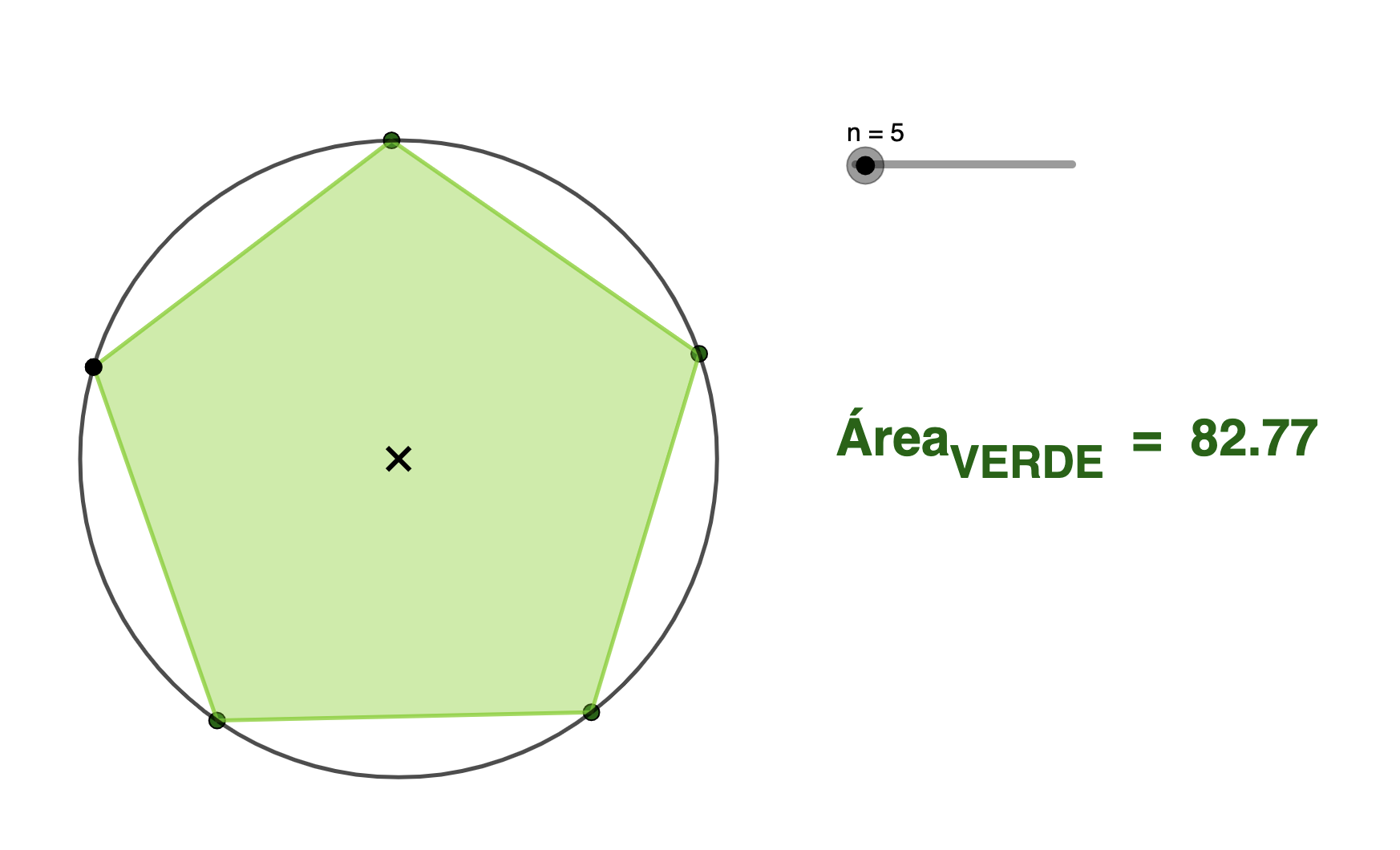
Comencemos calculando áreas.

El método de exahusión de Arquímedes
¿Quién fue Arquímedes?
Se considera que Arquímedes fue uno de los matemáticos más grandes de la antigüedad del siglo 3 A.C y, en general, de toda la historia.
Usó el método exhaustivo para calcular el área bajo el arco de una parábola con el sumatorio de una serie infinita, y dio una aproximación extremadamente precisa del número Pi.
También definió la espiral que lleva su nombre, fórmulas para los volúmenes de las superficies de revolución y un ingenioso sistema para expresar números muy largos.
Se considera que Arquímedes fue uno de los matemáticos más grandes de la antigüedad y, en general, de toda la historia. Usó el método exhaustivo para calcular el área bajo el arco de una parábola con el sumatorio de una serie infinita, y dio una aproximación extremadamente precisa del número pi. También definió la espiral que lleva su nombre, fórmulas para los volúmenes de las superficies de revolución y un ingenioso sistema para expresar números muy largos.