Utilizando las sumas de Riemman
Hasta ahora tenemos aproximaciones, muy buenas, pero aproximaciones en fin.
Como hemos visto a medida que aumentamos el número de intervalos a considerar para calcular las sumas inferiores y superiores, estas se aproximan cada vez más al valor del área buscada.
Las sumas superiores y inferiores forman lo que llamamos par de sucesiones monótonas convergentes. Y su límite, cuando n tiende a infinito es la integral.
Siempre y cuando estemos en las condiciones para que la función sea integrable... pero esas ya son otras historias.
Volvamos a verlo. Llamemos R(n) a la suma de Riemann para una cantidad de n de rectángulos y veamos como podemos aproximar:
∫6215x2
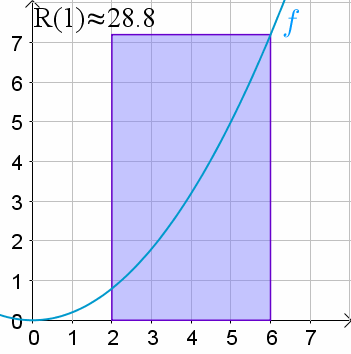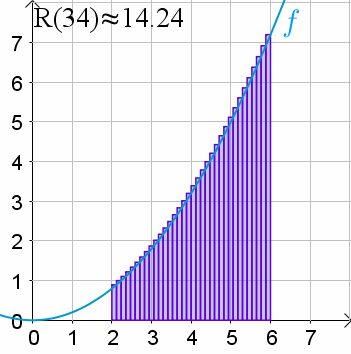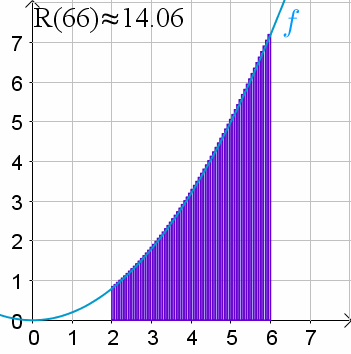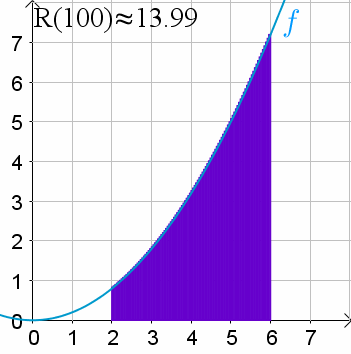
¿Qué tal que pudiéramos considerar una suma de Riemann con un número infinito de rectángulos?
Bueno, no podemos tomar porque el infinito no es un número, pero tal vez recuerdes que tenemos una forma de llevar algo a infinito...
¡¡Límites!!
Más en concreto este límite:
lim
Las sumas superiores y inferiores forman lo que llamamos par de sucesiones monótonas convergentes. Y su límite, cuando n tiende a infinito es la integral.
Siempre y cuando estemos en las condiciones para que la función sea integrable... pero esas ya son otras historias.