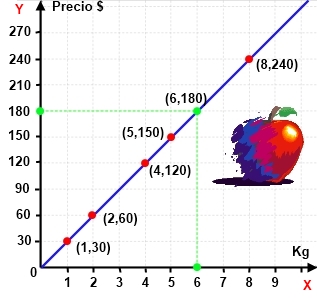
La gráfica de una función es el conjunto de todos los puntos obtenidos así:
- En el eje de abscisas (x) se representan los valores de la variable independiente (kg de manzanas) y en el de ordenadas (y) los de la dependiente (precio $).
- La primera coordenada de cada punto es cada uno de los valores de la variable independiente y la segunda, su imagen.
Para determinar a partir de la gráfica el valor de y = f(x) que corresponde a un valor de x concreto, por ejemplo 6 kg de manzanas, debemos trazar la recta perpendicular al eje X que pase por ese valor de x y el punto en el que esta recta corte a la gráfica es el valor de f(x).
Cada recta perpendicular debe cortar en un único punto a la gráfica, ya que en otro caso habría algún valor de x que tendría dos imágenes, lo cual no debe suceder.
La gran ventaja de la gráfica como forma de representar a una función es que proporciona una gran cantidad de información de un vistazo: nos dice cuál es el comportamiento global de la función, la tendencia que tiene, etcétera.
Por el contrario, como inconveniente se puede decir que, en general, es muy difícil obtener la gráfica precisa de una función cualquiera. De hecho, se necesita una herramienta matemática poderosísima para ello: el cálculo diferencial, combinado con el cálculo de límites funcionales.