Una tarde fría de invierno, Lucía trajo a su clase, un tangram diferente a los que habían trabajado, con el propósito de poder resolverlo junto a sus amigos en el recreo.

Este puzzle se conoce como el Cuadrado de Arquímedes o Stomachion y está formado por 14 piezas poligonales: 11 triángulos, 2 cuadriláteros y un pentágono, que juntos en alguna posición, forman un cuadrado.

El primer desafío será colocar las piezas en la posición correspondiente para completar el cuadrado: 

Si no puedes ver bien el recurso digital, visita https://www.geogebra.org/m/huvjgn87

Buscando información sobre este rompecabezas encontraron que el informático, Dr. Cutler, diseñó un programa para hallar las soluciones al problema. Y en el año 2003 reveló 536 formas para formar un cuadrado con las 14 piezas del puzzle. 

Ana los invita a aplicar el Teorema de Pick, para hallar la superficie de cada una de las piezas que conforman el Stomachion.  

Este teorema fué publicado por primera vez en 1899 por el matemático austríaco Georg Alexander Pick. Se establece una relación entre los puntos del Borde y del Interior de un polígono que se encuentre inscripto en una cuadrícula. 

Lo maravilloso de este resultado es que la fórmula es válida para cualquier polígono inscripto en una cuadrícula. 

Teorema de Pick

Dado cualquier polígono simple cuyos vértices se encuentran en una cuadrícula de enteros, su área, A, se calcula de acuerdo a la siguiente fórmula:

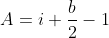
donde i es el número de puntos de cuadrícula dentro del polígono, b es el número de puntos de cuadrícula que se encuentran en el borde del polígono, y por 'simple' nos referimos a un polígono sin agujeros.